Wikipedia says
Personation is a term used in law for the specific kind of voter fraud where an individual votes in an election, whilst pretending to be a different elector.
when someone practices personation multiple times to cast multiple votes we are talking about ballot stuffing. In this post we will consider an election in which authentication is not 100% secure, where personation is difficult but not impossible. Furthermore we will assume there is some available, but costly method by which ballots can be audited to determine whether or not they were cast via personation or were in fact valid.
What makes the problem non trivial is that ballot auditing is costly and cannot in principle be performed for the entirety of the ballots cast. Hence we would like to estimate, from a limited number of audited ballots, how severe ballot stuffing was for an election. This estimation can be used either as a guarantee that all went well or in the opposite case to detect a problem and even invalidate the results.
What we need is a mathematical model that given some information about the results of an auditing processes allows us to estimate the proportion of “fake” ballots in the set of all those cast. In other words, we are talking about statistical inference; in this post will use a bayesian approach. Let’s get to work.
Imagine we have a box with all the ballots for an election, and the auditing process consists in randomly taking one out and determining whether it is valid or not, recording the result, and then repeating a limited number of times. After we have recorded the results of all the audits, we would like to know how many of ballots in the entire box are fake. Two things come to mind. First, that the result of each audit is binary, we either get FAKE or VALID. Second, that if the proportion of fake ballots in the box is p, then probability that a randomly chosen ballot is fake is p; the probability that it is valid is 1 – p.
The auditing process as a whole yields a count of fake ballots and a count of valid ballots. If we have probablity p for the result of a single audit , can we assign a probablity to the count resulting from the complete audit process? Yes, the binomial distribution and its brother the hypergeometric distribution do just that[1]. Here they are
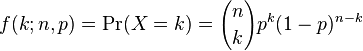
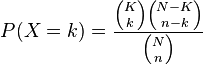
In our example, k above corresponds to the count of fake ballots. So these distributions give us a way to calculate the probability that a specific number of fake ballots is obtained in the audit assuming a certain proportion of fake ballots in the entire election. For example, let’s say we have 100 ballots total and we know that 10 of them are fake. What is the probability that if we audited 10 ballots we would obtain a fake count of 3?
P(X = 3) = 0.057395628 (binomial)
P(X = 3) = 0.0517937053324283 (hypergeometric)
Only 5%, it is unlikely we’d find 3 fake ballots with only 10 audits, given that there are only 10 out of 100 in total.
We have a way to calculate the probability of some outcome given some assumption about the proportion of fake ballots. But remember, what we want is exactly the opposite: given a certain result for an audit, we’d like to estimate the proportion of fake ballots in the entire set. It is this inversion that makes the problem a case of bayesian inference, and our friend Bayes theorem gives us the relationship between what we have and what we want.
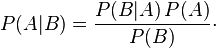
in our case, it translates down to
P(Proportion of fake ballots | Audit Result) = P(Audit Result | Proportion of fake ballots) * P(Proportion of fake ballots) / P(Audit Result)
What we were calculating before is P(Audit Result | Proportion of fake ballots), which we can plug into the formula, together with the other terms, to get what we want: P(Proportion of fake ballots | Audit Result). The other terms are
P(Audit Result) =
The unconditional probability that a certain audit result occurs. It can be calculated by summing over all possible proportions, like this version of Bayes theorem shows:

As seen in the bottom term. Because the bottom term is common to all values of Ai, it can be interpreted as a normalizing constant that ensures that probabilities sum to 1.
P(Proportion of fake ballots) =
The prior probability that some proportion of fake ballots occurs. This ingredient is crucial for Bayesian inference and the Bayesian approach in general. It is an estimate of the quantity we want to calculate that is prior to any of the evidence we obtain. It can be used to encode prior knowledge about what we are calculating. If we have no knowledge, we can try to encode that in a “neutral prior”. This last point is a very deep problem in Bayesian inference, as is the general problem of choosing priors. We won’t go into in detail here.
Recap. We want to calculate the proportion of fake ballots in an election based on the results of limited audits. We have seen how the binomial and hypergeometric distributions give probabilities for the results of an audit given an assumption about the proportion of fake ballots. Bayes theorem can be used to calculate the inverse probability that we are after, once we have specified a prior. See it in action in the next post.
[1] There is an important difference, the binomial distribution models sampling with replacement, whereas the hypergeometric models sampling without replacement. In the next post we will consider this difference and its significance for our problem.



















